大家好，我的麦洛克，有幸您能刷到我们这个微信。如果您对统计感兴趣，欢迎和着麦子一起来吃统计，本系列内容会带着您了解应用统计学的一个分支：医学应用统计。每次内容作用于一个信息点，从实际应用的角度出发，对医学应用统计进行分析讨论，所以过程中不刻意区分描述统计和推理统计的内容框架。

我们的微信课程结构，默认学生在大学本科或硕士阶段已经具备一定的概率论和统计学基础，当然，如果有需求，我们会在文中包含一些解释。

统计和英语一样，是工具，大家经历了这个过程，其实就这么回事。

目前的章节，我们从实际应用出发，解决我们医疗行业的样本量计算问题。从计量、计数以及诊断试验等几个维度来分述。之后，我们依据反馈，对一些具体工具及其使用进行介绍，如：生存分析Kaplan-Meier、ROC曲线分析制作、Bland-Altman方法学比较等，还有些比较基础的Pearson正态相关性、Spearman非正态等级相关性、单（多）变量回归分析等。

软件上，没有编程基础的同学可以参考Medcalc、有兴趣加深的同学，可以跟着我们的课程参与学习SAS，今天我们先讲一些基础概念，这对样本量计算（主要是推理统计）很重要。

******************************************************************************************************************

在临床试验设计中，研究者除了设计与药品或器械有关的评价细节，同时都非常关注的问题是：样本量。即在希望的把握度下得出具备有临床意义的差异，需要多少样本量？如果我们做了一批临床试验，其结果是否具有理想的把握度。

很多同学往往一上来，直接开问，我这个产品做个临床需要多少样本量。对于这类的问题，其实，说简单也简单，说难也不易。主要来自于具体的试验设计，我们说两个维度：统计设计和统计分析。在试验之前进行良好的统计设计，在获得数据后进行针对性的数据确认即统计分析。统计设计又会和药品或器械本身的特性、采用何种金标、目前临床入组操作的可行性等因素相关，所以在确定样本量之前，一定要对产品的前后情况做一些调查，至少要了解：

1） 该产品的上市临床应用情况（境内境外）；

2） 该产品及其同类产品的预期上市国家的器械信息；

3） 该产品的学术文献信息，最好是原产品或同类相似器械。

这些信息能够有效的帮助你了解，该类器械（后文中我们就用器械吧）在预期国家的临床预期的批准情况、是否有存在缺少金标或对比、甚至可以通过文献找到可以借鉴的临床方案等。所以不要上来一蹴而就。我们在设计方案时，有一些基础概念和信息，同学们要有所了解，今天我们把他们做些介绍和讲解。

计数资料：又称为定性资料或无序分类变量资料，也称名义变量资料，是将观察单位按某种属性或类别分组计数，分别汇总各组观察单位数后而得到的资料，其变量值是定性的，表现为互不相容的属性或类别。

计量资料：又称定量资料或数值变量资料，为观测每个观察单位某项指标的大小而获得的资料。其变量值是定量的，表现为数值大小，一般有度量衡单位。

（PS：当我们了解计数资料或计量资料后，可以据此分析使用不同的样本含量估算方法，比如：基于计量资料的t检验和F检验，基于计数资料的卡方检验和Fisher's精确检验等都有不同的样本含量估算方法。另外差异性检验、非劣效性检验和等效性检验也会对样本含量估算方法有影响。）

P值：是指在H₀规定的总体中进行随机抽样，所观察到的样本量及其更极端值的概率。P值也反映拒绝H₀犯I型错误的实际概率。P值也可以理解为结论的风险大小，也就是数据得出的结果有多大的错误风险。P值越小，结论错误的风险越小，即结论越可靠；P值越大，错误的风险越大，即结论的可靠性差。P值是对已有结果的错误风险判断，与结果大小无关。目前不少医学杂志上仍然存在着关于P值的不规范用语，如P≤0.05认为“差异显著”，P≤0.01认为“差异非常显著”等。不要将P值大小与实际差异大小联系起来。这是一个值得注意的地方。

如果P<0.01，说明是较强的判定结果，拒绝假定的参数取值。

如果0.01值<0.05，说明较弱的判定结果，拒绝假定的参数取值。

如果P值>0.05，说明结果更倾向于接受假定的参数取值。

检验水平α：也称显著性水平。指预先给定的判断小概率事件的概率尺度，假设检验结果下有差别结论的界值概率。I型错误表示，统计推断拒绝了实际上成立的无效假设(H0) . I型错误的概率用α表示，故又称α错误. 在这里I型错误指的是组间差异实际上不存在，统计推断的结果. 却错误地承认组间差异的存在，即假阳性。进行统计推断时，研究者需要对容许犯I 型错误的大小作出规定，通常是α≤0.05。因为在这一范围内，若作出拒绝H0的推断，其所犯的I 型错误概率已很小，故承认这一推断的正确性. 检验水平α值越小. 所需样本含量越大.

可信度：由1-α反应即计算出的区间包括总体均数μ的概率大小，其值越接近1越好。

检验效能(power，1-β)：统计学上称为检验效能，也称为把握度，表示当两总体确实有差别时，按规定的检验水平，能发现其差别的能力。II型错误表示，统计推断的结果不拒绝实际上不成立的H₀其出现的概率用β表示. 故也称为β错误. 或者说，当组间的差异确实存在时，统计推断却不承认该差异的存在，也称为假阴性。 β越小，所需要的样本量越大。根据实际情况，通常规定β≤0.10，必要时，可取β=0.20。把握度一般不大为人所重视，但当数据出现阴性结果的时候，你就会发现它的用处了。你可以用把握度判断一下阴性结果是否因为例数太少，如果是，你可以继续增加样本含量，如果不是，那就只好宣布实验结果事与愿违了。

变异(σ)：指样本中所包含的个体的差异程度。个体之间的差异越大，所需要的样本含量越大。反之，若个体之间的差异越小，则所需要观察的例数越少。差异往往相对于需要观察的亚组分析。

临床有意义的差值(δ)：临床有意义的差值也可称为组间效应的差异程度，即不同器械可能的疗效差异。组间差异越大，所需要的病例数越少. 反之，则所需要观察的病例数越多。

有时，当缺乏试验的疗效数据时，可以用我们希望得到的具有临床意义的差值来推测试验使用器械的疗效。

单侧检验与双侧检验：差异性检验和等效性检验需要双侧检验；而非劣效性检验和优效性检验可用单侧检验。一般单侧检验所需要的样本量少于双侧检验。单侧和双侧检验多用于组间比较。如果比较A、B两种器械的疗效，如果已预期B器械不可能不如A器械，则可以采用单侧检验。这种情形也常用于新药物与安慰剂之间比较，因为预期药物疗效往往不可能比安慰剂差，则可以用单侧检验。如果对两种药的疗效并不确定，B药可能优于A药，也可能劣与A药，则多采用双侧检验。

一般而言，如果事先对A、B两组了解不多，没有足够的证据了解A和B谁大谁小，就可选择双侧检验，如果事先了解谁大谁小，就可以选择单侧检验。值得注意的是：单侧检验和双侧检验的选择必须根据专业在数据分析之前确定。

某种角度而言，单侧检验比双侧检验更容易得到“有统计学意义”的结论，也就是更容易得到阳性结果。因此，切不可得到P值后再返回来选择有利的检验方式。

本次内容暂告段落，下面两张图，同学们可以比较感受一下。

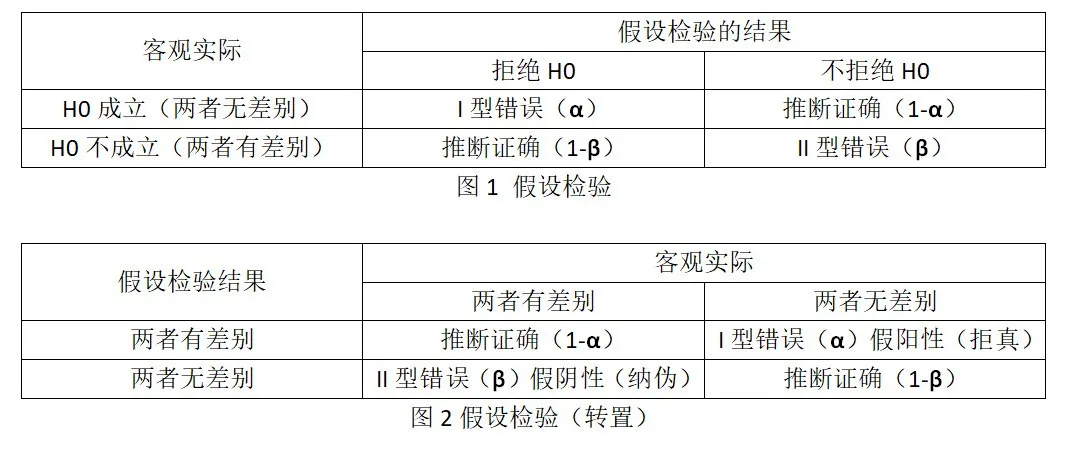
下期再见！